빅오(Big-O) 표기법

빅오

• 알고리즘의 성능을 수학적으로 표현해주는 표기법
• 시간과 공간복잡도를 표현할수 있다
• 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는게 목표 (상수는 무시)

O(1)

F(int[] n){
    return (n[0] == 0)? true:false;
}

• 입력 데이터 크기의 상관없이 일정한 시간이 걸리는 알고리즘
• 인자로 받는 배열 값이 얼마나 큰지 상관없이 일정한 속도로 반환한다

O(1)

O(n)

F(int[] n){
    for i = 0 to n.length
        print i 
}

• 입력데이터 크기에 비례해서 처리시간이 걸리는 알고리즘
• n개의 데이터를 받으면 n번 루프돌아서 n이 1씩 늘어날때마다 처리가 한번씩 늘어난다

O(n)

O(n²)

F(int[] n){
    for i = 0 to n.length
        for j = 0 to n.length
            print i + j;
}

O(n²)

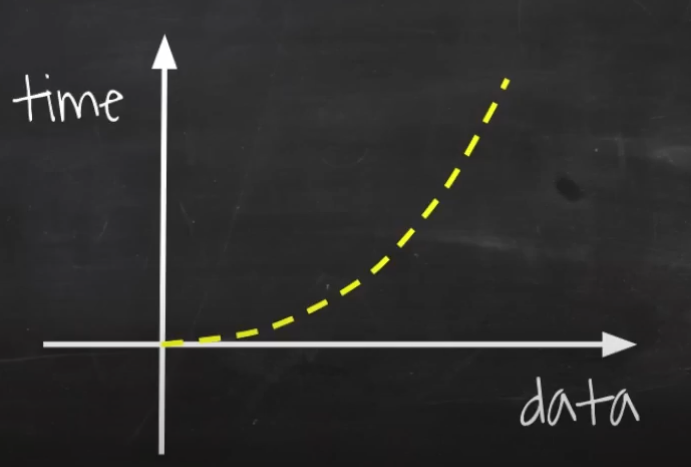
• 첫번째 루프에서 n번 돌면서 각각의 엘리먼트에서 n번씩 또 돌면서 n을 가로세로 길이로 가지는 면적만큼 늘어난다
• n이 늘어날때마다 아래한줄 오른쪽 한줄씩 늘어나게 된다

O(nm)

F(int [] n, int[] m){
    for i = 0 to n.length
        for j = 0 to m.length
            print i + j;
}

O(nm)

O(n³)

F(int[] n){
    for i = 0 to n.length
        for j = 0 to n.length
            for k = 0 to n.length
                print i + j + k
}

O(n³)

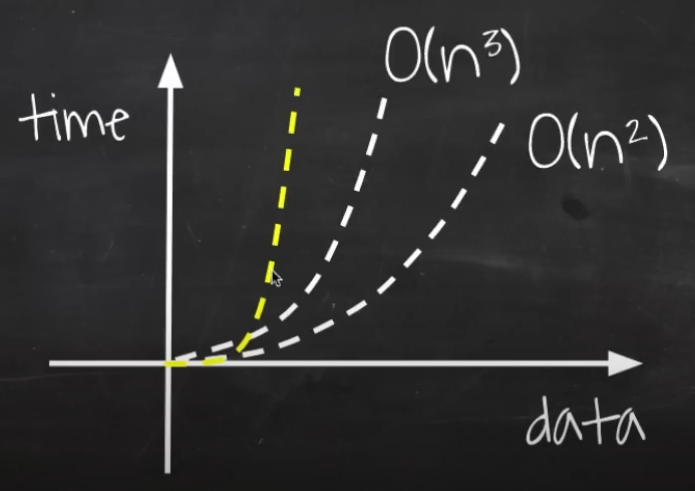
• O(n²) 을 n 만클 돌리면서 상자모양이 된다 
• 데이터가 증가함에 따라 O(n²) 보다 급격하게 증가된다

O(2ⁿ)

F(n, r) {
	if (n<=0) return 0;
    else if (n == 1) return r[n] = 1;
    return r[n] F(n-1, r) + F(n-2, r);
    
}

O(2ⁿ)

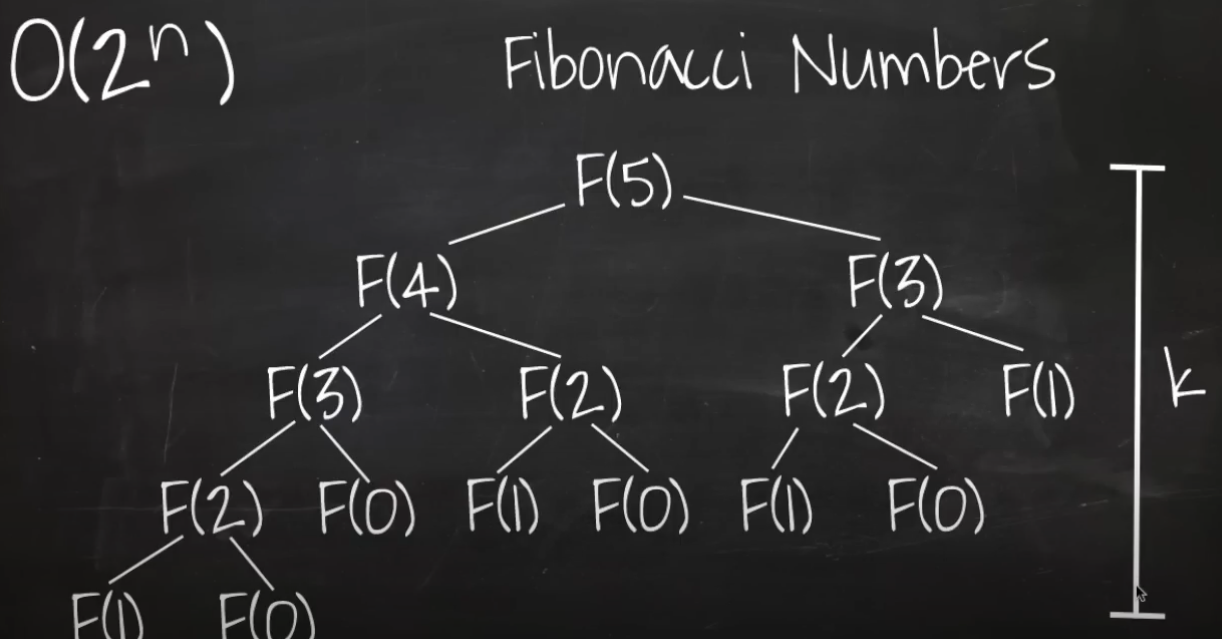
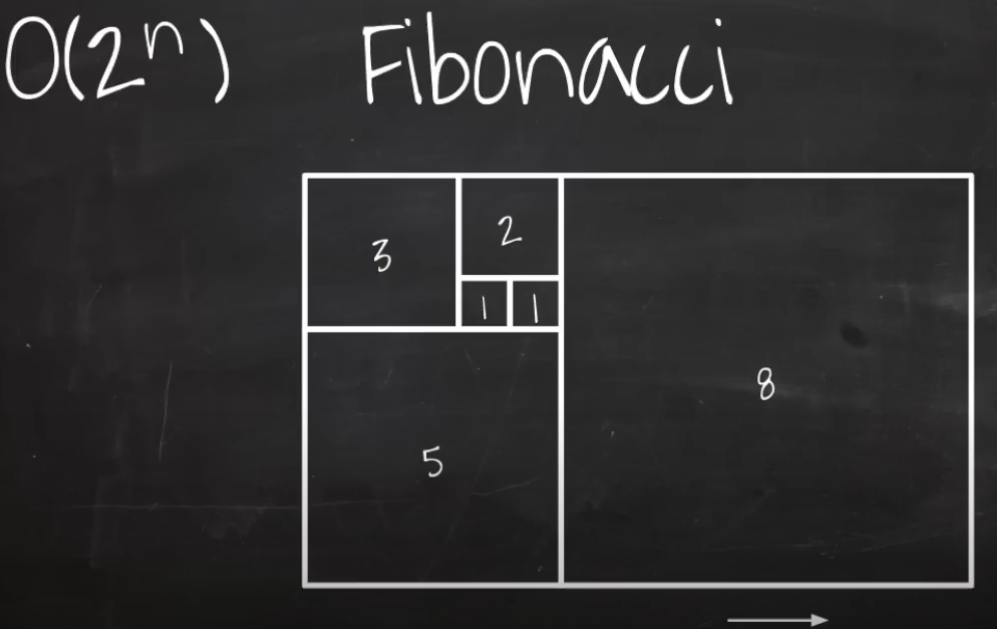
• 함수를 호출할때마다 이전숫자와 전전 숫자를 알아야 더할수 있다 
• 하나뺀 숫자로 재귀호출하고 두개뺀 숫자로 재귀호출한다
• 매번함수가 호출될때마다 2번씩 호출되고 트리의 높이(k) 만큼 반복한다

O(log n)

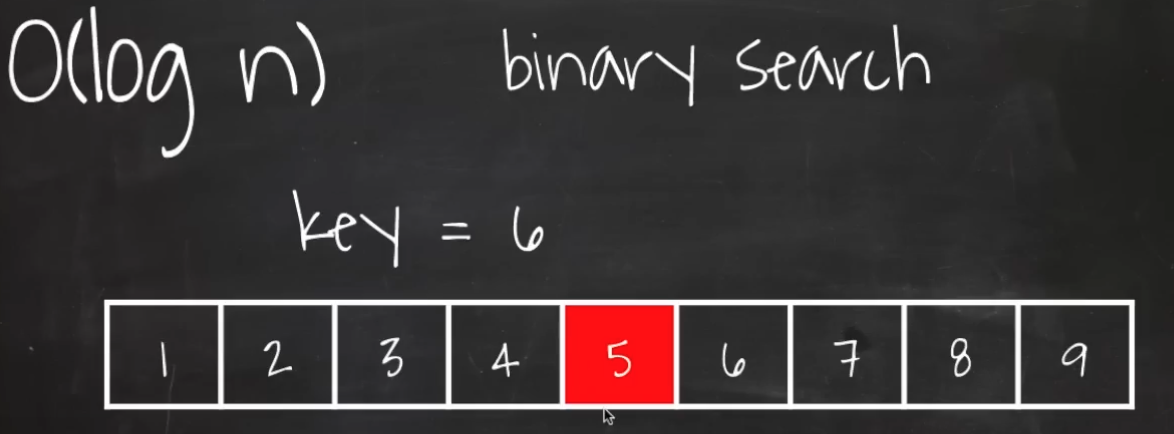
• 대표적인 이진검색 가운데 값을 찾아서 key값과 비교한다
• 가운데 값이 key 보다 작기때문에 앞쪽 값은 비교 안해도 된다 

 

 

 

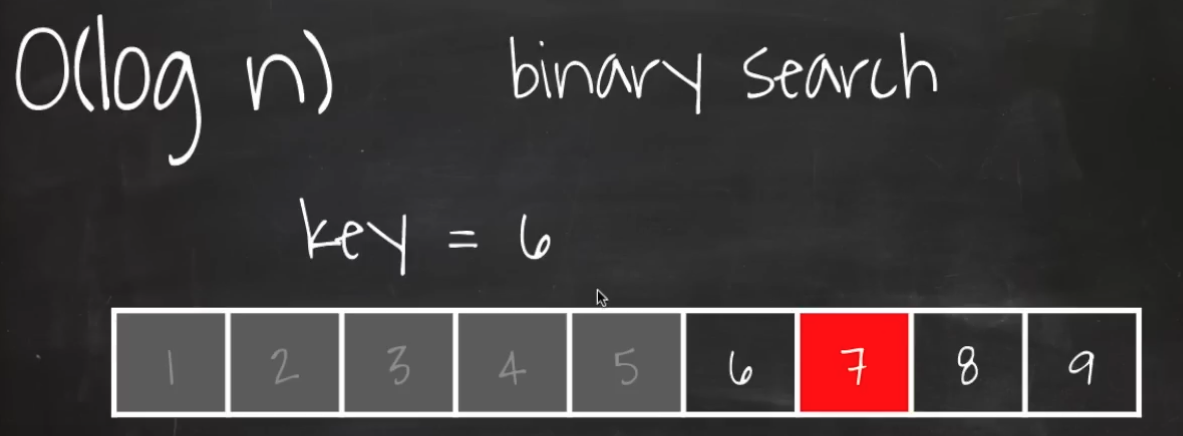
• 7은 key 값보다 작기때문에 뒷쪽 값은 비교를 안해도된다

 

 

 

 

 

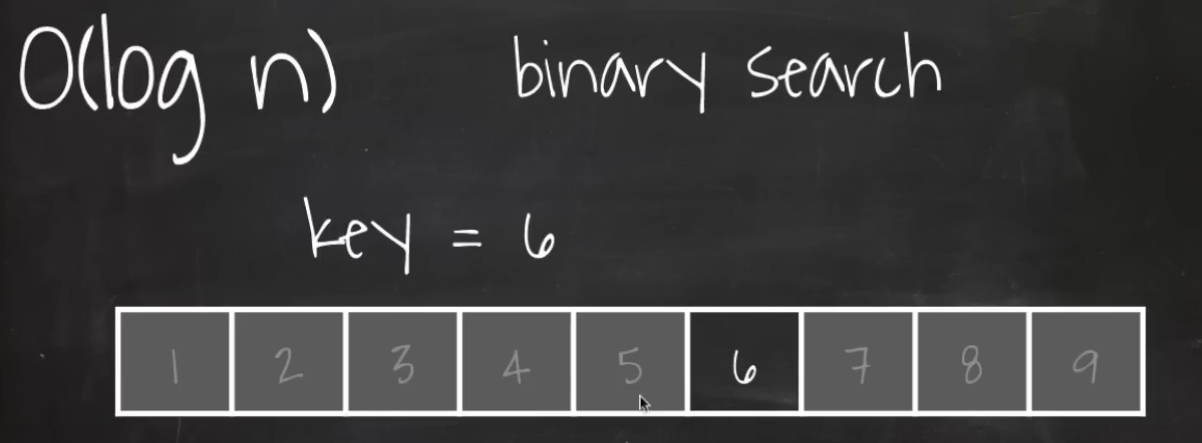
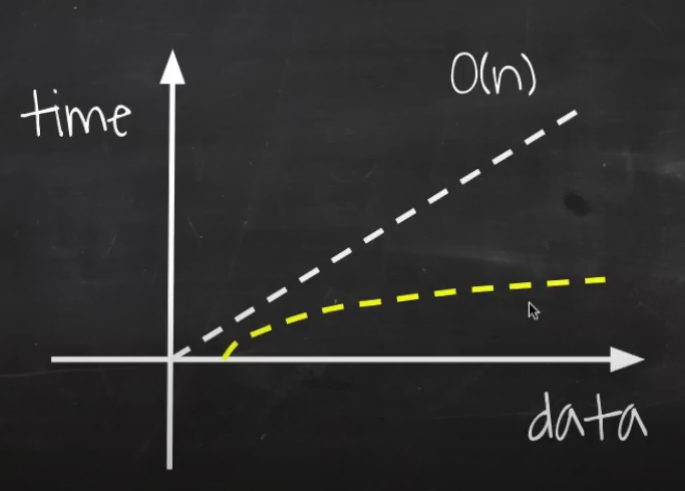
• 검색해야 하는 데이터의 양이 절반씩 떨어지는 알고리즘음 O(log n) 이라고 한다

 

 

 

 

F(k, arr, s, e) {
	if(s>e) return -1;
    
    m = (s+e) / 2; //중간값
    
    if(arr[m] == k) return m;
    else if(arr[m] > k) return F(k, arr, s, m-1); // 중간값보다 작을경우
    else return F(k, arr, m+1, e); // 중간값보다 클경우
}

O(log n)

상수는 무시하자

F(int [] n){
	for i = 0 to n.length
    	print i
    for i = 0 to n.length
    	print i
}

• O(2n) => O(n)
• 빅오 표기법은 데이터 증가에 따른 처리시간율을 예측하기 위해 만들어진 표기법
• 상수는 고정된 숫자 이기 때문에 증가율을 영향에 미칠때 고정된 상수 만큼 영향을 미치기 때문에 무시한다