자료구조

목차

1.자료구조
2.선형구조
3.비선형구조
4.폴리쉬표기법변환

---

1.자료구조

1-1. 자료구조의 개념

* 프로그램에서 쉽게 활용될수 있도록 논리적으로 설계된 데이터의 구조 및 관계를 의미
* 같은 데이터라도 데이터 구조를 어떻게 구성하는지에 따라 성능에 많은 영향을 미침
* 효과적인 자료구조는 데이터 용량과 실행 시간등을 최소한으로 사용
* 데이터의 추가, 삭제, 탐색을 보다 효율적으로 연산하는 활동도 포함

1-2. 자료구조의 유형

1. 단순구조
    * 프로그래밍 언어에서 제공하는 기본 데이터 타입
    * 정수형, 실수형, 문자형
2. 선형구조(Linear)
    * 데이터들의 대응관계가 1:1로 구성되는 구조
    * 순차구조: 삽입과 삭제시간이 많이 소요되는 선형구조
    * 연결구조: 삽입과 삭제가 효율적으로 이루어지는 선형구조
    * Stack, Queue, Deque, Linear List, Linked List
3. 비선형구조(Non-Linear)
    * 데이터들의 대응 관계가 1:N, N:M 구성되는 구조
    * 트리(Tree): 1:N 관계를 계층적으로 나타낸 비선형구조
    * 그래프(Graph): N:M 관계를 그물망 형태로 나타낸 비선형 구조
    * Tree, Graph
4. 파일구조
    * 보조 기억 장치에 데이터 값이 실제로 기록되는 자료구조
    * 순차파일, 색인파일

---

2.선형구조

2-1. 스택(Stack)

1. 스택의 구조
    * 데이터의 입구와 출구가 같아서 삽입과 삭제가 한쪽에서만 일어나는 구조
    * 스택포인터* 가장 마지막에 삽입된 데이터의 위치를 가리킨다
    * 스택포인터는 삽입(PUSH) 될때마다 1씩 증가하며 스택크기를 넘으면 오류(Overflow) 발생
    * 스택포인터는 추출(POP) 될때마다 1씩 감소하며 0보다 작아지면 오류(Overflow) 발생
2. 스택의 특징
    * LIFO: 가장 나중에 삽입된 데이터가 가장 먼저 추출되는 후입선출
    * 함수호출, 우선탐색, 재귀호출, Linear List, Post-fix 사용

스택(Stack)

2-2. 큐(Queue)

1. 큐의 구조
    * 데이터의 입구와 출구가 달라서 삽입과 삭제가 반대쪽에서 일어나는 구조
    * 삽입 포인터(Rear)가 저장된 데이터중 가장 마지막에 삽입된 데이터의 위치
    * 삽입 포인터는 데이터가 입력될때마다 1씩 증가하며 큐의 크기를 넘어서게 되면 오류(Overflow) 발생
    * 삭제 포인터(Front)가 저장된 데이터중 가장 처음에 삽입된 데이터의 위치를 가리킨다
    * 삭제 포인터는 데이터를 삭제할때마다 1씩 증가하며 삽입포인터와 같은 위치를 가리키게 되며 큐에 데이터가 비어있는 상태가 된다
2. 큐의 특징
    * FIFO: 가장 먼저 삽입된 데이터가 가장 먼저 출력되는 선입선출
    * 프린터 스풀이나 입출력 버퍼와 같은 대기행렬에 적합한 자료구조

큐(Queue)

2-3. 데크(Deque)

1. 데크의 구조
    * 데이터의 출입구가 양쪽 모두에 있는 구조
    * 각각의 포인터(Left, Right)가 데이터 삽입, 삭제에 따라 1씩 증가하거나 감소
2. 데크의 특징
    * 입출력 제한 유형에 따라 스크롤 방식과 쉘프 방식이 있다
    * 입력 제한 데크(Scroll): 출력은 양쪽에서 가능하지만 입력은 한쪽에서만 가능
    * 출력 제한 데크(Shelf): 입력은 양쪽에서 가능하지만 출력은 한쪽에서만 가능

데크(Deque)

2-4. 선형리스트

1. 선형리스트 특징
    * 동질형 데이터가 연속되는 기억공간에 저장되는 데이터 구조
    * 가장 간단한 구조이며 접근속도가 비교적 빠르다
    * 삽입, 삭제시 나머지 자료들의 이동이 필요하기 때문에 시간이 오래걸린다
    * 선형 리스트의 대표적인 구조에는 배열(Array) 있다
2. 배열의 특징
    * 같은 데이터 타입의 요소들이 같은 크기의 공간에 순차적으로 나열되어 있는 구조
    * 같은 이름을 사용하고 첨자에 의해 서로의 위치를 구분
    * 데이터 탐색에 가장 효과적인 자료구조
    * 배열의 데이터 삽입 
    * 배열의 데이터 삭제

 

2-5. 연결리스트

1. 연결 리스트의 특징
    * 데이터의 삽입과 삭제가 어려운 배열의 단점을 보완한 자료구조
    * 데이터의 삽입과 삭제가 용이하며 기억공간이 연속적이지 않아도 문제가 없다
    * 데이터마다 포인터가 필요하므로 기억공간이 추가로 필요하며 탐색속도는 비교적 느린편이다
2. 연결 리스트의 구조
    * 데이터와 포인터를 묶어서 노드라고 표현
    * 임의의 기억공간에 생성된 노드들이 각 노드의 포인터에 의하여 연결
    * 중간 노드의 연결이 끊어지면 다시 복구할수 없다
3. 연결 리스트의 종류
    * 단일 연결리스트
    * 원형 연결리스트
    * 이중 연결리스트
    * 이중 원형 연결리스트

---

3.비선형 구조

3-1. 트리(Tree)

1. 트리구조의 특징
    * 데이터를 계층구조로 표현하기에 적합한 자료구조
    * 하나이상의 노드를 가지며 각 노드는 간선으로 연결
    * 방향성이 있는 비순환 그래프의 한종류
2. 트리구조의 종류
    * 이진트리: 자식노드의 수가 최대 2개인 트리
    * 포화이진트리: 모든레벨에서 노드가 꽉채워진 이진트리
    * 완전이진트리: 마지막 레벨을 제외한 모든 레벨의 노드가 꽉채워진 이진트리
3. 트리의 용어
    * 근(Root) 노드: 부모가 없는 노드
    * 단말(Leaf) 노드: 자식이 없는 노드
    * 내부(Internal) 노드: 단말노드가 아닌 노드
    * 간선(Edge, Link, Branch): 노드를 연결하는 선
    * 형제(Sibling) 노드: 같은 부모를 갖는 노드
    * 노드의 크기(Size): 자신이 부모노드인 서브쿼리의 노드개수
    * 노드의 깊이(Depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
    * 트리의 높이(Height): 트리의 최대 노드 깊이 + 1
    * 노드의 레벨(Level): 같은 깊이를 가지는 노드의 집합
    * 노드의 차수(Degree): 자식 노드의 개수
    * 트리의 차수(Degree Of Tree): 트리의 최대 차수
4. 이진트리순회 : 트리의 모든 노드를 한번씩 방문하는 행위
    * 중위 순회(In-Order)
        - 좌측자식 -> 부모 -> 우측자식
    * 전위 순회(Pre-Order)
        - 부모 -> 좌측자식 -> 우측자식
    * 후위 순회(Post-Order)
        - 좌측자식 -> 우측자식 -> 부모

트리(Tree)

3-2. 그래프(Graph)

1. 그래프의 개념
    * 노드를 간선으로 연결하여 관계를 표현할수 있는 자료구조
    * 방향, 무방향 그래프가 존재
    * 자체간선, 순환그래프, 비순환그래프 모두 존재
    * 순환하므로 루트노드, 부모, 자식노드 개념이 없다
2. 그래프의 용어
    * 정점(Vertex): 위치(Node 같은 개념)
    * 간선(Edge, Link, Branch): 노드를 연결하는 선
    * 인접 정점(Adjacent Vertex): 간선에 의해 직접 연결된 정점
    * 정점의 차수(Degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
    * 진입 차수(In-Degree): 방향 그래프에서 외부에서 오는 간선의 수
    * 진출 차수(Out-Degree): 방향 그래프에서 외부로 향하는 간선의 수
    * 경로의 길이(Path Length): 경로를 구성하는 사용된 간선의 수
    * 단순 경로(Simple Path): 경로중에서 반복되는 정점이 없는 경우
    * 사이클(Cycle): 단순경로의 시작 정점과 종료정점이 동일한 경우
3. 방향 그래프
    * 무방향 그래프의 간선은 간선을 통해서 양방향으로 갈수 있다
    * 정점 A와 정점 B를 연결하는 간선은 (A, B)와 같이 정점의 쌍으로 표현
        - (A, B) 는 (B, A) 동일
    * 방향성 완전 그래프의 최대 간선의 수
        - n(n-1)
        - 완전그래프: 모든정점에 간선이 연결된 그래프
4. 무방향 그래프
    * 간선에 방향성이 존재하여 한 방향으로 진행되는 그래프
    * A -> B로만 갈수있는 간선은 <A, B> 표시
        - (A, B) 는 (B, A) 서로 다른방향
    * 무방향 완전 그래프의 최대 간선의 수
        - n(n-1)/2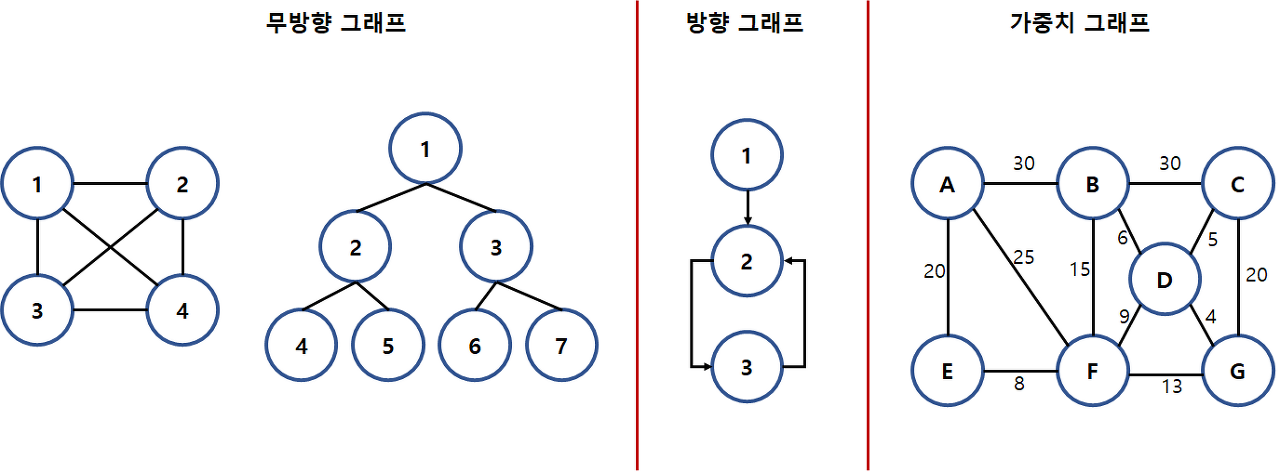

그래프(Graph)

4.폴리쉬 표기법 변환

4-1. 폴리쉬 표기법의 종류

1. 중위식(Infix): 연산자가 피연산자들의 중간에 위치하는 형식
2. 전위식(Prefix): 연산자가 피연산자들의 앞쪽에 위치하는 형식
3. 후위식(Postfix): 연산자가 피연산자들의 뒤쪽에 위치하는 형식

4-2. 중위식을 전위식으로 변환

* 연산순위가 빠른 연산부터 전위식으로 변환한후 하나의 그룹으로 묶는다
* 해당 그룹과 그다음 연산을 차례차례 전위식으로 변환
* (A-B)*C+D 전위식 변환
    -AB
    *(-AB)C
    +(*-ABC)D
    +*-ABCD

4-3. 중위식을 후위식으로 변환

* 연산순위가 빠른 연산부터 후위식으로 변환한후 하나의 그룹으로 묶는다
* 해당 그룹과 그다음 연산을 차례차례 전위식으로 변환
* (A-B)*C+D 후위식 변환
    AB-
    (AB-)C*
    (AB-C*)D+
    AB-C*D+

4-4. 전위식을 중위식으로 변환

* 전위식의 형태(연산자, 피연산자)를 중위식으로 변환한후 하나의 그룹으로 묶는다
* 해당 그룹과 그 다음 연산을 차례차례 중위식으로 변환
* +*-ABCD 중위식으로 변환
    A-B
    (A-B)*C
    (A-B)*C+D

4-5. 후위식을 중위식으로 변환

* 후위식의 형태(피연산자, 연산자)를 중위식으로 변환한후 하나의 그룹으로 묶는다
* 해당 그룹과 그 다음 연산을 차례차례 중위식으로 변환
* AB-C*D+ 중위식으로 변환
    A-B
    (A-B)*C
    (A-B)*C+D

참고자료 : 이기적 환상콤비 정보처리기사